階乗と分割数の漸近挙動―スターリングの公式とハーディ・ラマヌジャンの定理
#数楽 弱っているときには雑談(と書いて「すうがく」と読む)。Stirlingの公式を最短で示すにはガンマ函数そのものに「定積分∫exp(f(x))dxの値にはf(x)の大きな所の寄与が大きい」というLaplaceの方法を適用するのが簡単。その方法は素朴だけど極めて有用。続く
#数楽 続き。しかし、ガンマ函数のより深い解析のためおよび様々な分野との関係を知るためには、ガンマ函数そのものだけではなく、「その対数の漸近挙動を調べる」という「いつもの方法」を適用してみることも大事。所謂(Stirling-)Binetの公式の話。続く
#数楽 Γ函数の無限積展開より(トリガンマ函数):=(log Γ(s))''=Σ_{n=0}^∞ 1/(n+s)^2となることを出発点に積分して行く話。Whittaker-Watsonの引き写しが http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … 第8.5節にあります。
#数楽 メモhttp://ocw.nctu.edu.tw/course/fourier/supplement/gamma-2.pdf …An Elementary Proof of Binet's Formula for the Gamma FunctionZoltin Sasvari
#数楽 q-Stirling公式もq-Γ函数についてq-Binet公式の形で証明されています。たとえば http://cm00.epage.au.edu.tw/ezfiles/7/1007/img/2542/29(3)7-1(285-293).pdf … の(1.3)式の類がそれ。
#数楽 q-Stirlingについてググると、Tsallisエントロピーとの関連文献もヒットしますが、Tsallisの意味での"q-"は所謂q解析の意味での"q-"とは異なるので注意。その話の解説を http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … の8.3〜8.6節に書いた。
#数楽 メモhttp://mnishi.my.coocan.jp/mnishi/thesis.pdf …Generalization of Gamma Function and Its Applications to q-AnalysisMichitomo Nishizawa
#数楽 「それそのものではなく、その対数を考える」と言えば、Taoさんによる色々なRiemann予想の解説もRiemannゼータ函数の対数微分の話から始めて、合同ゼータ函数の話をに繋げていましたね→ https://terrytao.wordpress.com/2013/07/19/the-riemann-hypothesis-in-various-settings/ …
#数楽 Tsallisエントロピーの話についても色々調べてみたのですが、全然理解できませんでした。Tsallis系の話は、log(x)のh類似(q=1+h)としてl(x)=(x^h-1)/hを、exp(y)の類似としてe(y)=(1+hx)^{1/h}を考える話です。続く
#数楽 通常の(相対)エントロピーは多項分布のn→∞での漸近挙動の記述に自然に現われること(Sanovの定理)から、それが普遍的に出て来る理由がよくわかるのですが、Tsallis的な話ではそういうことがよくわからない。私自身の分からなさの度合は先の私のノートを見ればわかります。
#数楽 Re:self-RTsStirlingの公式n!〜n^n e^{-n}√(2πn)Hardy-Ramanujanの定理p(n)~exp(π√(2n/3))/(4√3 n)ここでp(b)は分割数これらの公式では定数因子まで正確に求まっている。
#数楽 Stirlingの公式の素朴な見方の1つ→「1からnまでの数を重複を許してランダムにn個選ぶとき、n個の数字が互いに異なる確率は√(2πn)/e^nで近似される」1/e^nだけで挙動をかなりわかった気になれるが、より精密に√(2πn)までわかっている点がうれしい。
#数楽 「1からnまでの数を重複を許してランダムにn個選ぶとき、n個の数字が互いに異なる確率」という稀なことが起こる確率はおおよそnの指数函数分の1の速さで小さくなることが、√(2πn)/e^nの中の1/e^nの部分からわかります。√nの影響は相対的に小さい。
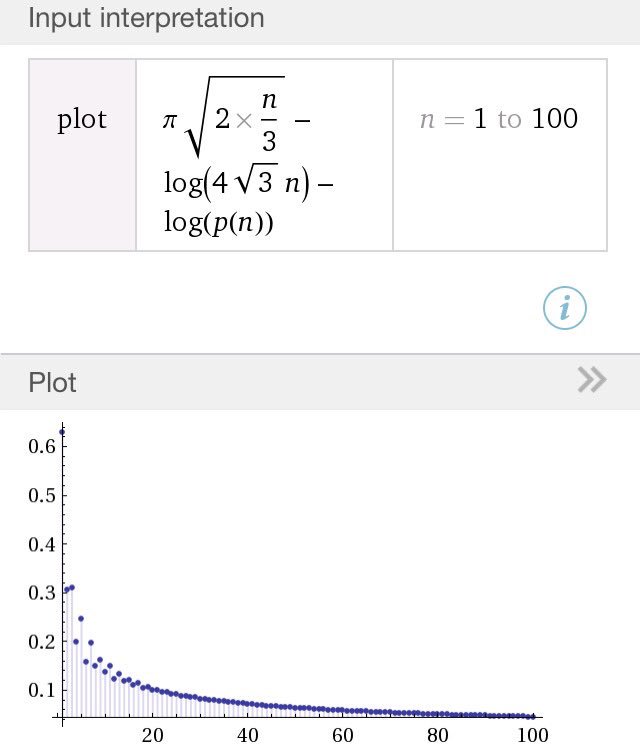
#数楽 Hardy-Rananujanの定理の数値的確認。[exp(π√(2n/3))/(4√3 n)]/p(n) の対数をプロット。n→∞で0に収束。http://www.wolframalpha.com/input/?i=plot%20y=π√(2n/3)-log(4√3 n)-log(PartitionP(n)), 1
#数楽 Hardy-Ramanujanの定理から、分割数p(n)の対数はおおよそnの平方根オーダーで増加することがわかるが、log(4√3 n)の項までわかっているのがうれしい。(Stirlingの公式の場合と同様にもっと精密な結果が得られている。)

#数楽 添付画像中の[In]は http://www.jstor.org/stable/1970462 です。 pic.twitter.com/oFz5dRpRMgモジュラー変換性から係数の漸近挙動を得るTauber型定理!
#数楽 http://projecteuclid.org/download/pdf_1/euclid.mmj/1028998729 …これはNewmanさんによる分割数に関するHardy-Rananujanの定理のsimplified proof. 最後は分割数p(n)を近似する数列q(n)の定積分表示にLaplaceの方法を適用する。
#数楽 たぶんNewmanさんの方針でInghamさん[In]のモジュラー変換性から係数の漸近挙動を出すTauber型定理も証明できると思うので、誰かそういう解説文を書いてくれないかなあ(もしくは見つけて来てくれないかなあ)と思っています。
#数楽 漸近挙動を見るときには、影響が大きな因子から順番に記述して行くのが定跡なのですが、以上でしたことは、最初のnの指数函数部分exp(nS)の部分のSを記述するだけで非常に役に立つという話。
#数楽 exp(nS+O(log n))のO(log n)を無視してよいとみなすことは、大体においてC n^a exp(nS)のC n^aの部分を無視することになるので、ぎょっとすることもあるかもしれませんが、「C n^aはexp(nS)と比較すると1に近い」で問題ない。

#数楽 分割数に関するHardy-Ramanujanの定理:p(n)~exp(π√(2n/3))/(4√3 n) as n→∞.添付画像中のIngham [In] は http://www.jstor.org/stable/1970462 pic.twitter.com/oFz5dRpRMg
#数楽 Inghamさんの論文ではη函数分の1の漸近挙動からその係数(=分割数)の漸近挙動を得るためにTauber型定理を証明して使っています。η函数の漸近挙動はそのモジュラー変換性から得られる。漸近挙動を調べるためのモジュラー変換性の利用は由緒正しい使い方かも。
#数楽 NewmanさんによるHardy-Ramanujanの定理の別証明(1962)http://projecteuclid.org/euclid.mmj/1028998729 …Hardy-Ramanujanの定理では、指数函数部分exp(π√(2n/3))だけではなく、1/(4√3 n)の部分まで精密に求まっている。
#数楽補題2:a_nが正値数列でΣ_{n=0}^∞ a_n x^n〜1/(1-x)^α (x↑1)ならばΣ_{k=1}^n a_k〜n^α/Γ(α+1) (n→∞).Laplace変換版はKaramataの方法を使えば易しい。和分版はそれに帰着。続く
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



